• Программа Решение Дифференциальных Уравнений Методом Эйлера В Mathcad
• Программа Решение Дифференциальных Уравнений Методом Эйлера В Excel

Численное решение уравнения методом Эйлера и Рунге-Кутта в Excel. Программа на языке Turbo Pascal. Тема: Решение дифференциальных уравнений по методу Эйлера. Тип: Курсовая. В работе есть. Рассматривается линейное однородное дифференциальное уравнение второго. Методы Эйлера и Рунге-Кутта, следует свести это уравнение к системе 2-х. На отрезке t=[0.1] с шагом 0,01 в среде Maple (текст программы).

Одношаговые методы Многошаговые методы Кафедра физхимии ЮФУ (РГУ) ЧИСЛЕННЫЕ МЕТОДЫ И ПРОГРАММИРОВАНИЕ Материалы к лекционному курсу Лектор – ст. РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Постановка задачи При решении научных и инженерно-технических задач часто бывает необходимо математически описать какую-либо динамическую систему.

Лучше всего это делать в виде дифференциальных уравнений ( ДУ) или системы дифференциальных уравнений. Наиболее часто они такая задача возникает при решении проблем, связанных с моделированием кинетики химических реакций и различных явлений переноса (тепла, массы, импульса) – теплообмена, перемешивания, сушки, адсорбции, при описании движения макро- и микрочастиц.

Обыкновенным дифференциальным уравнением (ОДУ) n-го порядка называется следующее уравнение, которое содержит одну или несколько производных от искомой функции y(x):, здесь y (n) обозначает производную порядка n некоторой функции y(x), x – это независимая переменная. В ряде случаев дифференциальное уравнение можно преобразовать к виду, в котором старшая производная выражена в явном виде. Такая форма записи называется уравнением, разрешенным относительно старшей производной (при этом в правой части уравнения старшая производная отсутствует): (6.1) Именно такая форма записи принята в качестве стандартной при рассмотрении численных методов решения ОДУ. Линейным дифференциальным уравнением называется уравнение, линейное относительно функции y(x) и всех ее производных. Например, ниже приведены линейные ОДУ первого и второго порядков Решением обыкновенного дифференциального уравнения называется такая функция y(x), которая при любых х удовлетворяет этому уравнению в определенном конечном или бесконечном интервале. Процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.

Общее решение ОДУ n-го порядка содержит n произвольных констант C 1, C 2, C n Это очевидно следует из того, что неопределенный интеграл равен первообразной подынтегрального выражения плюс константа интегрирования Так как для решения ДУ n-го порядка необходимо провести n интегрирований, то в общем решении появляется n констант интегрирования. Частное решение ОДУ получается из общего, если константам интегрирования придать некоторые значения, определив некоторые дополнительные условия, количество которых позволяет вычислить все неопределенные константы интегрирования. Точное (аналитическое) решение (общее или частное) дифференциального уравнения подразумевает получение искомого решения (функции y(x)) в виде выражения от элементарных функций. Это возможно далеко не всегда даже для уравнений первого порядка. Численное решение ДУ (частное) заключается в вычислении функции y(x) и ее производных в некоторых заданных точках, лежащих на определенном отрезке.

То есть, фактически, решение ДУ n-го порядка вида получается в виде следующей таблицы чисел (столбец значений старшей производной вычисляется подстановкой значений в уравнение): X y y' y (n-1) x 1 y(x 1) y'(x 1) y (n-1)(x 1) x 2 y(x 2) y'(x 2) y (n-1)(x 2) x N y(x N) y'(x N) y (n-1)(x N) Например, для дифференциального уравнения первого порядка таблица решения будет представлять собой два столбца – x и y. Множество значений абсцисс в которых определяется значение функции, называют сеткой, на которой определена функция y(x). Сами координаты при этом называют узлами сетки. Чаще всего, для удобства, используются равномерные сетки, в которых разница между соседними узлами постоянна и называется шагом сетки или шагом интегрирования дифференциального уравнения или, i = 1, N Для определения частного решения необходимо задать дополнительные условия, которые позволят вычислить константы интегрирования. Причем таких условий должно быть ровно n. Для уравнений первого порядка – одно, для второго - 2 и т.д.

В зависимости от способа их задания при решении дифференциальных уравнений существуют три типа задач: Задача Коши (начальная задача): Необходимо найти такое частное решение дифференциального уравнения, которое удовлетворяет определенным начальными условиям, заданным в одной точке: то есть, задано определенное значение независимой переменной (х 0), и значение функции и всех ее производных вплоть до порядка (n-1) в этой точке. Эта точка (х 0) называется начальной. Например, если решается ДУ 1-го порядка, то начальные условия выражаются в виде пары чисел (x 0, y 0) Такого рода задача встречается при решении ОДУ, которые описывают, например, кинетику химических реакций. В этом случае известны концентрации веществ в начальный момент времени ( t = 0), и необходимо найти концентрации веществ через некоторый промежуток времени ( t). В качестве примера можно так же привести задачу о теплопереносе или массопереносе (диффузии), уравнение движения материальной точки под действием сил и т.д. Краевая задача.

В этом случае известны значения функции и (или) ее производных в более чем одной точке, например, в начальный и конечный момент времени, и необходимо найти частное решение дифференциального уравнения между этими точками. Сами дополнительные условия в этом случае называются краевыми ( граничными) условиями. Естественно, что краевая задача может решаться для ОДУ не ниже 2-го порядка. Ниже приведен пример ОДУ второго порядка с граничными условиями (заданы значения функции в двух различных точках): Задача Штурма-Лиувиля (задача на собственные значения). Задачи этого типа похожи на краевую задачу.

При их решении необходимо найти, при каких значениях какого-либо параметра решение ДУ удовлетворяет краевым условиям (собственные значения) и функции, которые являются решением ДУ при каждом значении параметра (собственные функции). Например, многие задачи квантовой механики являются задачами на собственные значения. Численные методы решения задачи Коши ОДУ первого порядка Рассмотрим некоторые численные методы решения задачи Коши (начальной задачи) обыкновенных дифференциальных уравнений первого порядка. Запишем данное уравнение в общем виде, разрешенном относительно производной (правая часть уравнения не зависит от первой производной): (6.2) Необходимо найти значения функции y в заданных точках сетки, если известны начальные значения, где есть значение функции y(x) в начальной точке x 0. Преобразуем уравнение умножением на dx И проинтегрируем левую и правую части между i-ым и i+1-ым узлами сетки. (6.3) Мы получили выражение для построения решения в i+1 узле интегрирования через значения x и y в i-ом узле сетки. Сложность, однако, заключается в том, что интеграл в правой части есть интеграл от неявно заданной функции, нахождение которого в аналитическом виде в общем случае невозможно.

Численные методы решения ОДУ различным способом аппроксимируют (приближают) значение этого интеграла для построения формул численного интегрирования ОДУ. Из множества разработанных для решения ОДУ первого порядка методов рассмотрим методы,.

Они достаточно просты и дают начальное представление о подходах к решению данной задачи в рамках численного решения. Метод Эйлера Исторически первым и наиболее простым способом численного решения задачи Коши для ОДУ первого порядка является метод Эйлера. В его основе лежит аппроксимация производной отношением конечных приращений зависимой ( y) и независимой ( x) переменных между узлами равномерной сетки: где y i+1 это искомое значение функции в точке x i+1. Если теперь преобразовать это уравнение, и учесть равномерность сетки интегрирования, то получится итерационная формула, по которой можно вычислить y i+1, если известно y i в точке х i: (6.4) Сравнивая формулу Эйлера с общим выражением, полученным ранее, видно, что для приближенного вычисления интеграла в в методе Эйлера используется простейшая формула интегрирования - формула прямоугольников по левому краю отрезка.

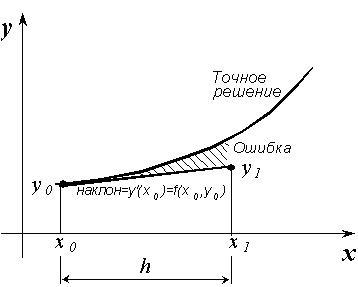
Графическая интерпретация метода Эйлера также не представляет затруднений (см. Рисунок ниже). Действительно, исходя из вида решаемого уравнения следует, что значение есть значение производной функции y(x) в точке x=x i -, и, таким образом, равно тангенсу угла наклона каcательной, проведенной к графику функции y(x) в точке x=x i. Из прямоугольного треугольника на рисунке можно найти, откуда и получается формула Эйлера.

Таким образом, суть метода Эйлера заключается в замене функции y(x) на отрезке интегрирования прямой линией, касательной к графику в точке x=x i. Если искомая функция сильно отличается от линейной на отрезке интегрирования, то погрешность вычисления будет значительной. Ошибка метода Эйлера прямо пропорциональна шагу интегрирования: Ошибка  h Процесс вычислений строится следующим образом. При заданных начальных условиях x 0 и y 0 можно вычислить Таким образом, строится таблица значений функции y(x) с определенным шагом ( h) по x на отрезке x 0, x N. Ошибка в определении значения y(x i) при этом будет тем меньше, чем меньше выбрана длина шага h (что определяется точностью формулы интегрирования). При больших h метод Эйлера весьма неточен.

Он дает все более точное приближение при уменьшении шага интегрирования. Если отрезок x i, x i+1 слишком велик, то каждый участок x i, x i+1 разбивается на N отрезков интегрирования и к каждому их них применяется формула Эйлера с шагом, то есть шаг интегрирования h берется меньше шага сетки, на которой определяется решение. Пример: Используя метод Эйлера, построить приближенное решение для следующей задачи Коши: На сетке с шагом 0,1 в интервале 0, 1 (6.5) Решение: Данное уравнение уже записано в стандартном виде, резрешенном относительно производной искомой функции.

Поэтому, для решаемого уравнения имеем Примем шаг интегрирования равным шагу сетки h = 0,1. При этом для каждого узла сетки будет вычислено только одно значение ( N=1). Для первых четырех узлов сетки вычисления будут следующими: И т.

Полные результаты (с точностью до пятого знака после запятой) приведены в в третьей колонке - h=0,1 ( N=1). Во второй колонке таблицы для сравнения приведены значения, вычисленные по аналитическому решению данного уравнения. Во второй части таблицы приведена относительная погрешность полученных решений. Видно, что при h=0,1 погрешность весьма велика, достигая 100% для первого узла x=0,1. K λ l 2 3/2 -1/2 3 23/12 -16/12 5/12 4 55/24 -59/24 37/24 -9/24 Полученное таким образом семейство формул называется явной k-шаговой схемой Адамса ( методы Адамса-Башфорта). Например, четырехшаговая явная формула Адамса может быть записана так: Если для построения интерполяционного полинома использовать k узлов, начиная с x i+1, то можно получить формулы интегрирования ОДУ, известные как неявные схемы Адамса (или методы Адамса-Моултона).

Неявными эти формулы называются потому, что значение искомой функции в (i+1)-м узле - y i+1 - оказывается одновременно и в левой и правой частях равенства. Квадратурные коэффициенты для неявных методов Адамса приведены в таблице ниже. K λ l 2 1/2 1/2 3 5/12 8/12 -1/12 4 9/24 19/24 -5/24 1/24 Например, четырехшаговая неявная формула Адамса-Моултона имеет вид: Видно, что это выражение является уравнением относительно y i+1, так как y i+1 встречается и в левой и правой его части. Однако обычно это уравнение не решается, а значение в правой части заменяется на рассчитанное по какой-либо явной формуле - например, формуле Адамса-Башфорта.

Такой подход лежит в основе. Достоинством многошаговых методов Адамса при решении ОДУ заключается в том, что в каждом узле рассчитывается только одно значение правой части ОДУ - функции F(x,y). К недостаткам можно отнести невозможность старта многошагового метода из единственной начальной точки, так как для вычислений по k-шаговой формуле необходимо знание значения функции в k узлах. Поэтому приходится (k-1) решение в первых узлах x 1, x 2, x k-1 получать с помощью какого-либо одношагового метода, например метода. Другой проблемой является невозможность изменения шага в процессе решения, что легко реализуется в одношаговых методах.

Методы прогноза и коррекции Несколько иной подход используется в многошаговых методах прогноза и коррекции. В качестве иллюстрирующего примера рассмотрим 2-х шаговый метод прогноза и коррекции. Пусть дано ДУ для которого известно значение функции в двух соседних узлах сетки: Сначала строится прогноз значения в (i+1)-ом узле интегрирования по какой-либо грубой формуле (при k=2 это метод Эйлера) по предудущему узлу. Затем это значение корректируется по более точной формуле, в данном случае – по формуле трапеций ( неявная формула Адамса второго порядка) В качестве решения в узле x i+1 берется где E c- ошибка коррекции Для того чтобы начать расчет методом прогноза и коррекции, необходимо знать значения функции в двух первых узлах сетки - x 0 и x 1 -. Обычно значение в узле x 1определяется каким-либо одношаговым методом ( или ).

На каждом шаге построения решения методом прогноза и коррекции требуется вычислить всего одно значение функции, а одно берется из предыдущего узла сетки. Поэтому он весьма экономичен по затратам времени вычислений при достаточной точности. Погрешность описываемого метода пропорциональна h 3 (d  h 3).

Аналогичные схемы прогноза-коррекции могут быть получены сочетанием явных (прогноз) и неявных (коррекция) формул Адамса для различных k. Так, например, широко применяется четырехшаговый метод прогноза-коррекции, в котором в качестве прогноза используется 4-х шаговая формула, а для коррекции - 4-х шаговая формула Адамса-Моултона. Погрешность такого метода пропорциональна h 5. Пример: С использованием алгоритма прогноза и коррекции второго порядка решить ДУ в точке x 2 = 0,2 при h = 0,1 со следующими начальными значениями: Решение: При h = 0,1 получаем Аналитическое решение уравнения (с точностью до 9 знака после запятой) дает значение y(0,2) =0,018730753. Относительная погрешность составляет 0,049%. Решение задачи Коши для систем дифференциальных уравнений 1-го порядка Системой M дифференциальных уравнений первого порядка в общем случае можно назвать следующую совокупность Обыкновенных дифференциальных уравнений:, Где есть некоторые функции независимой переменной х, причем правые части уравнений не зависят от производных y i(x), то есть все уравнения разрешены относительно производных функций. Начальными условиями при решения задачи Коши для такой системы будут являться значение независимой переменной и значения всех M функций при этом значении: Все описанные ранее методы решения задачи Коши для уравнений легко обобщаются на случай решения систем ДУ первого порядка.

Формулы выбранного метода применяются последовательно к каждому уравнению системы уравнений для определения значения соответствующей функции. Из первого уравнения определяется значение y 1 i, из второго – y 2 i, из M-го - y Mi. В качестве примера рассмотрим применение 4-го порядка для решения системы двух ОДУ первого порядка. Адаптируем формулу для данной системы уравнений. Из первого уравнения будем вычислять значения функции u( x), а из второго – функции v( x) (это функции, чьи производные стоят в левой части соотетствующих уравнений): Аналогично для второго: С учетом вышесказанного, для расчета коэффициентов k u0 - k u3 используем правую часть первого уравнения ( F 1), а для коэффициентов k v0 - k v 3 - второго ( F 2). Кроме этого, для расчета приращения функции u используем коэффициенты k u, а для расчета приращения функции v - k v.

Таким образом, коэффициенты рассчитываются по следующим формулам: Модель 'хищник-жертва' Примером задачи, сводимой к системе нелинейных дифференциальных уравнений 1-го порядка, является задача 'хищник — жертва'. Данная модель довольно широко применяется при описании временной зависимости объема популяций в биологических системах, при моделировании экономических и физических процессов. Задача формулируется следующим образом. Пусть в системе в некоторый момент времени t имеются хищники (например, волки) в количестве v( t) и жертвы (например, зайцы) в количестве u( t).

Модель 'хищник — жертва' утверждает, что u( t) и v( t) удовлетворяют системе ОДУ первого порядка: Где A, B, C и D – некоторые числовые константы. Действительно, если зайцы имеют достаточно травы для питания, то скорость роста популяции будет прямо пропорциональна их числу (первое слагаемое в первом уравнении). Второе слагаемое описывает гибель зайцев при встрече с хищниками, так как вероятность их встречи равна произведению. Второе уравнение описывает изменение популяции хищников. Скорости роста популяции способствует их хорошее питание (первое слагаемое второго уравнения пропорционально вероятности встречи хищника и жертвы - ), а избыток хищников приводит к их гибели за счет голода (второе слагаемое). Применим метод Рунге-Кутты 4-го порядка для решения полученной системы уравнений.

Сравнивая и систему, записанную в, заметим, что: Тогда выражения для расчета коэффициентов k u0 - k u3 и k v0 - k v 3 принимают следующий вид: Значения функций u и v находятся по уже известным формулам: Решение задачи Коши для дифференциальных уравнений второго и более высоких порядков Задачу Коши для ОДУ второго порядка, можно свести к решению системы двух ДУ первого порядка, если ввести некоторую функцию тогда и система примет вид при начальных условиях Аналогично, ОДУ порядка n сведется к системе из n дифференциальных уравнений первого порядка. Движение тела под действием пружины Рассмотрим некоторое материальное тело массой m, которое движется по горизонтальной поверхности (в общем случае – с трением) под действием пружины.

Сила упругого сжатия (растяжения) пружины описывается законом Гука и пропорциональна смещению тела от положения равновесия пружины ( x = 0): k – коэффициент жесткости пружины. Сила трения направлена всегда против движения тела и пропорциональна его скорости: с – коэффициент трения.

1 Численные методы решения обыкновенных дифференциальных уравнений Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции (x y. Общий вид дифференциального уравнения первой степени: (n F(x, y, y.,y 0 ( Наивысший порядок производной n называется порядком дифференциального уравнения. Уравнение первого порядка F(x, y, y 0 второго порядка F(x, y, y,y 0., В ряде случаев из общей записи дифференциального уравнения удается выразить старшую производную в явном виде: y y f(x, y f(x, y, y Такая форма записи называется уравнением, разрешенным относительно старшей производной. ( Линейное дифференциальное уравнение это уравнение, линейное относительно искомой функции и ее производных. Например, линейное уравнение первого порядка. Y x y sn x Решением дифференциального уравнения называется всякая функция y (x, которая после ее подстановки обращает уравнение в тождество. Общее решение обыкновенного дифференциального уравнения n-го порядка содержит n произвольных постоянных: C,C., Cn y (x,c,c.,cn.

Имеет вид: 2 Частное решение получается из общего, если произвольным постоянным придать определенное значения. Например, для уравнения первого порядка общее решение зависит от одной произвольной постоянной, т.е. Оно имеет вид: y (x,c (4 Если C принимает определенное значение C C0 решение: y (x,c 0, где C 0 =сonst., то получаем частное Общее решение y (k, C описывает бесконечное семейство интегральных кривых с параметром C. Частному решению соответствует одна кривая из этого семейства. Эта кривая проходит через заданную точку x 0, y 0. Здесь 0, y0 x начальное условие.

Такой тип задач, где задаются начальные условия, называется задачей Коши. Если дополнительные условия для получения частного решения задаются более чем в одной точке, т. При разных значениях переменной x, то такая задача называется краевой, а сами дополнительные условия при этом называются граничными. Примеры постановки задач: y; x а Задача Коши: y x, x, y(, y( 0 б Краевая задача: y y y sn x, 0 x, y(0, y( 0. Методы решения обыкновенных дифференциальных уравнений подразделяются на: графические используют геометрические построения (метод изоклин; аналитические (точные; приближенные используют различные упрощения (асимптотический метод, разложение в ряд по малому параметру; численные решение на вычислительной технике. 3 МЕТОД ЭЙЛЕРА Это простейший численный метод решения задач Коши. Его недостаток большая погрешность.

Пусть дано дифференциальное уравнение первого порядка: Начальные условия: x0 y f(x,y (5 x, y y0. Этот метод относится к группе одношаговых методов, в которых для расчета точки y требуется информация только о последней вычисленной точке y. Формула Эйлера вычисления любого y такова y y h f ( x, y, где =0., n- (6 О точности вычисления. Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h и погрешность с учетом более точного значения h y. при шаге оценивают так:. max y y E для =., n; (7 E точность вычисления.

Вычисления в Excel по методу Эйлера Найти решение уравнения методом Эйлера в Mcrosoft Excel y 0,5y x (8 c начальным условием y ( 0 на отрезке 0;0,5 с шагом 0. Точность решения принять E 0, 000. Вычисления будут выполняться по соотношениям (следуют из формулы 6: y y h (0,5y x шагом 0, h; (9. h.

y (0,5 y y x шагом 0, 05 h. 5 Исправленный и модифицированный методы Эйлера Метод Эйлера можно усовершенствовать множеством различных способов.

Из этих способов наиболее распространены два. Это так называемые исправленный и модифицированный методы Эйлера. Обозначим и оба метода опишем формулой f ( x, y ( y y h ( x, y, ( ( x, y a a f ( x b h, y b h, ( Для исправленного метода a 0, 5 a и b b.

Для модифицированного метода 0, a a и b b 0, 5. Проведем для сравнения здесь решение той задачи исправленным методом Эйлера. С учетом функции (8 соотношение (4 выглядит так: f ( x, y 0, y x (4 5 На изображении отведем столбец A под значения x. Столбец B отведем под значения y, для выделим столбец C, столбец D под значения ( x, y. Формулы и вычисления на листе Excel показаны на следующих изображениях ( и 4. Формулы вычисления по исправленному методу Эйлера. 6 Изображение 4.

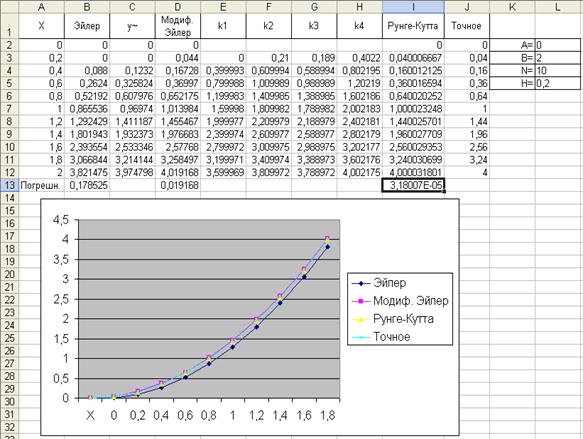
Вычисления по исправленному методу Эйлера Теперь перенесем эти соотношения по исправленному методу Эйлера на лист с вычислениями по методу Эйлера для сопоставимости результатов. При этом произведем дполнительные вычисления по исправленному методу Эйлера с шагом 0, 05 h. Изображение 5. Сравнение метода Эйлера и исправленного метода Эйлера Метод Рунге-Кутта четвертого порядка По этому одношаговому методу вычисления проводятся по формуле y y h ( x, y, (5 x, y 6 4 (, (6 f ( x, y, h h f ( x, y. 7 h h f ( x, y, 4 f ( x h, y h Решим предыдущий пример y 0,5y x методом Рунге-Кутта. Лист с формулами показан на двух избражениях (6 и 7. Изображение 6.

Формулы для вычисления по методу Рунге-Кутта Изображение 7. Формулы для вычисления по методу Рунге-Кутта (продолжение Приведем комментарий этого листа. Так, отведем блок ячеек А:А8 под значения x с шагом 0. Соответственно, в столбце В будем вычислять y, а в столбцах С,D,E,F - значения коэффициентов, 4. Столбец G отведем под ( x, y.

Формулы, которые необходимо вносить в ячейку вручную выделены желтым фоном. Содержимое остальных ячеек получается. 8 копированием из строк и 4. Результаты вычисления приведены на изображении 8. Изображение 8.

Вычисления по методу Рунге-Кутта для шага 0, Для сопоставления точности метода на изображении 8 приведены вычисления с шагом h 0,05. Изображение 9. Вычисления по методу Рунге-Кутта для шага 0,05 9 РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Рассмотренные одношаговые методы могут быть использованы для решения систем обыкновенных дифференциальных уравнений или для нахождения решения одного дифференциального уравнения высокого порядка.

В последнем случае введением новых переменных оно сводится к решению системы дифференциальных уравнений первого порядка. Рассмотрим решение задачи Коши применительно к системам таких уравнений. Задача Коши Для получения однозначного решения системы дифференциальных уравнений должны быть заданы дополнительные условия. Их должно быть задано столько, каков порядок решаемой системы.

Если все эти условия задаются в одной точке, т.е. При одном значении x x0, то такая задача называется задачей Коши. Эти дополнительные условия называются начальными условиями, а x 0 называется начальной точкой. Покажем применение метода Рунге-Кутта четвертого порядка для решения задачи Коши системы двух уравнений вида dy f( x, y, (6 d f( x, y, Начальные условия зададим в виде ( x0 y 0 y и ( x0 0. Запишем формулы Рунге-Кутта для приближенного решения этой системы где y L y h 4 6 h L L4 L 6 10 f x, y, L f x, y, L ( f (, x h y h hl, f (, x h y h hl, f (, x h y h hl, L (, f x h y h hl, L 4 4 h (, hl f, x h y, h (, hl f, x h y. ( В этих формулах 0, n. Для оценки погрешности используется правило двойного пересчета точно так же, как и при решении одного уравнения.

К решению подобной системы уравнений можно свести решение задачи Коши для уравнения второго порядка: d y f x, y, dy (7 с начальными условиями y ( x0 y 0. Y ( x 0 0 Введем новую переменную dy x. Заменяется следующей системой из двух уравнений с начальными условиями ( x0 y 0 (.

Тогда исследуемое уравнение (7 d f ( x, y, (8 dy (x (9 y и ( x0 0. Пример Применяя метод Рунге-Кутта, вычислить на отрезке ;,5 таблицу значений решения уравнения y y 0 x y (0. 11 с начальными условиями y ( 0, 77 и ( 0, 5 y выбрав шаг 0. С помощью подстановки новой переменной, перейдем к решению системы уравнений: y ( y x с начальными условиями y ( 0, 77 и ( 0, 5. Откроем новый рабочий лист Excel (изображение 8 и выделим в нем столбцы А, В и С под переменные x, y.

Изображение 0. Оформление листа В последующих столбцах будем вычислять значения, L. Пусть значения x помещаются в блок А:А8 (шаг по x составляет 0. Тогда в ячейки В и С занесем начальные значения y ( и (. Формулы, которые необходимо ввести вручную в остальных ячейках строк и 4 выделены в таблице серым фоном на изображении.

Программа Решение Дифференциальных Уравнений Методом Эйлера В Mathcad

12 Изображение. Оформление листа Формулы в остальных строках получаются путем копирования. Результаты решения задачи приведены на следующем изображении.

Программа Решение Дифференциальных Уравнений Методом Эйлера В Excel

Также там показан график зависимости y (x. График функции y(x Или в увеличенном формате: 13 Решение этого уравнения в Mathcad 14 Теперь решим ту же систему исправленным методом Эйлера. Напомним саму систему уравнений: -е уравнение dy d Начальные условия y ( 0, 77 и ( 0, 5 x. Y -е уравнение Итерации для -го уравнения: y y h ( x, y, ( ур ( ур ( x, y, a a( b h ( ( ур ( ур ур a a 0,5 и b b Итерации для для -го уравнения: h ( x, y, ( ур.